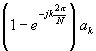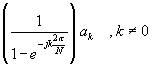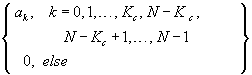A
real, N-periodic, discrete-time
signal x[n] can be represented as a discrete-time Fourier series
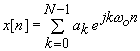
where
, and the discrete-time fundamental
frequency is 
.
The
complex coefficients 
can be calculated
from the expression
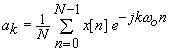
The
are called the spectral coefficients of the signal x[n].
A plot of 
vs k is called the magnitude spectrum of x[n],
and a plot of 
vs k is called the phase spectrum of x[n].
These plots, particularly the magnitude spectrum, provide a picture of the
frequency composition of the signal. Recall that the spectral coefficients
for a periodic signal repeat according to
.
The
applet below illustrates properties of the discrete-time Fourier series. You
can enter a value of N up to 15
and specify x[n] by sketching the signal or by sketching magnitude and
phase spectra with the mouse. Then standard operations can be performed on x[n]
and the effects on the signal and its spectra are displayed.
(Click the Reset button between operations.)
Let
y[n] be the signal resulting
from an operation on x[n], and let the discrete-time Fourier series
coefficients of y[n] be specified by 
. The table below lists the operations available, where M and
are integers and c
is a real constant. For the ideal low pass filter, 
specifies the highest
frequency, 
, that is passed by the filter. For the ideal low pass
filter, 
specifies the lowest
frequency passed by the filter.
Operation
|
Resulting signal y[n] |
Spectral coefficients k=0, 1,…, N-1 |
|
Amplitude Scale |
c x[n] |
|
|
Time Shift |
x[n – M] |
|
|
Time Scale* |
|
|
|
Time Reverse |
x[- n] |
|
|
First Difference |
x[n] - x[n-1] |
|
|
Running Sum** |
x[n]+ x[n-1]+ x[n-2]+¼ |
|
|
Ideal Low Pass |
filtered version of x[n], cutoff frequency |
|
|
Ideal High Pass |
filtered version of x[n], cutoff frequency |
|
of y[n]
* For this time scaling, the period of y[n]
is 2N.
** For the running sum,
y[n] is periodic if and only if 
.
