
We can also write y(t) as the product of x(t) and p(t), where p(t) is the unit-amplitude rectangular pulse of width 2T centered at t = 0. Then the Fourier transform relationship is a convolution:
Via either expression, the magnitude and phase spectra of y(t) are related to the magnitude and phase spectra of x(t) in a rather complicated fashion.
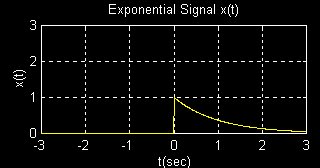
Compare the two exponential signals


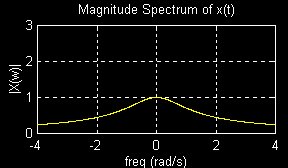
with the corresponding magnitude spectra

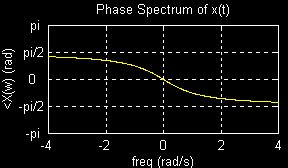
and phase spectra