Motivation: Main Research
As the observing technologies (sensors, cameras, camcorders, etc.) have matured over the years and the difficulties of data sharing have decreased, the amount of observation data has become immensely available (see this YouTube Video of swarm of starlings by National Geographic). My research is motivated by the need of making valid, useful and swift scientific discoveries from observation. For example, the story of how universal law of gravity was discovered traced back to Kepler's work on observation data of Mars' orbit.
To make a more precise statement of my research, the focus of my research is about designing and developing effective and efficient algorithms for making such discoveries. There are two major directions about my research:
- Infer dynamical structure from time-dependent obervations: Learning Dynamics
- Recover hidden variables from their noisy observations: Data Recovery
In order to make accurate, convergent, and effective algorithms, I use theories and techniques from machine learning, numerical ODE/PDE, scientific computing, approximation theory, inverse problems, probability and statistics. Oftentimes, due to the gigantic size of the data set, the algorithms have to be scalable and efficient, hence I employ various techniques which reduce computing time: multi-scale representation, iterative solver, dimension reduction, domain decomposition, parallel computing, GPU computing (check out the Code section for details), etc. My research is interdisciplinary, it requries concrete knowledge of the observation technologies and underlying system, and it has applications in physics, biology, social science, and related engineering fields.
[ Back to top ]
Motivation: Learning Dynamics
Dynamical systems have been used to model and describe complex physical, biological, social, and economical phenomena, see here. We are interested in developing and analyzing data-driven methods in deriving, validating, and improving complex dynamical system modeling. We are especially interested in a special kind of dynamical systems, namely the collective dynamics. It is also known as self-organized dynamics, as it displays self-organization in the system. The study of collective dynamics is driven by the need to understand some of the basic collective behaviors in bacterium, animals, human beings and even AI-controlled robots, such as flocking, milling, swarming, and rendezvous. Moreover, we are also interested in studying how emergent behaviors (clustering, flocking, milling, swarming, synchronization, etc.) appear in collective dynamics from observation data.
We developed a non-parametric learning approach to infer interaction laws (how agents interact with each other in the collective dynamics setting) in [1] as an extension of the paper, Inferring interaction rules from observations of evolutive systems I: the variational approach, by Maggioni, et al. We design and develop the learning program, and we show that it is well-posed, with excellent converngence properties as well as performance guarantees on how well our estimators are predicting the governing structure of the dynamical system, and the dynamical trajectories over the training time interval. We also tested several semi-supervised learning cases (model-selection) in order to showcase the excellent predication capability of our estimators.
In [2], we focus on expanding the learning approach proposed in [1] in three major directions: to study the large-time behavior of our estimators, to expand the learning of more complex dynamical systems (dynamics with 2-variable dependence interaction laws), and to discover hidden parametric stucture from the estimators.
In [3], we apply our method in learning gravitational dynamics to student some of the important historical astronomical events (discovery of precession of Mercury's orbit as well as general relativity effects on Mercury's orbit) from the current NASA JPL's Horizons data on our Solar system.
In [4], we provide convergence analysis of the expanded systems introduced in [2].
In [5], we extend our learning approach to collective dynamics on non-Euclidean manifolds, and investigate the convergence property of our estimators on these manifolds, taking into account the geometric properties of the dynamics.
In [6], we study the optimal way of building hypothesis spaces (local/global dictionaries) for learning dynamical systems.
List of publications in learning dynamics:
- F. Lu, M. Zhong, S. Tang, M. Maggioni. Nonparametric inference of interaction laws in systems of agents from trajectory data (arXiv page), PNAS, 116 (3), 14424 - 14433, June 2019.
- M. Zhong, J. Miller, M. Maggioni. Data-driven Discovery of Emergent Behaviors in Collective Dynamics (arXiv page), Physica D: nonlinear phenomenon, 411, 132542, October 2020.
- M. Maggioni, J. Miller, M. Zhong. Semi-supervise Learning of Celestial Dynamics from Modern Ephemeris, In Preparation.
- J. Miller, S. Tang, M. Zhong and M. Maggioni. Learning theory for inferring interaction kernels in second-order interacting agent systems, submitted (arXiv page).
- M. Maggioni, J. Miller, H. Qiu, M. Zhong. Learning interaction kernels for agent systems on Riemannian manifolds, submitted (arXiv link available upon request).
- F. Lu, M. Maggioni, M. Zhong. Adaptive Kernel Learning of Dynamical Systems, In Preparation.
[ Back to top ]
Examples -- Opinion Dynamics
The Opinion Dynamics (OD) studies how people's opinions interact with each other and how consensus is formed. It was first introduced as a discrete model by U. Krause in his paper, "a discrete nonlinear and non-autonomous model of consensus formation", in 2000. S. Motsch and E. Tadmor in their 2014 paper, "heterophilious dynamics enhances consensus", gave a very good summary of various kinds of opinion dynamics and extension.


[ Back to top ]
Examples -- Lennard-Jones Dynamics
The Lennard-Jones Dynamics (LJ) uses an interaction law which is induced by a Lennard-Jones potential. It is used mostly in studying molecule formation and other molecular dynamics in quantum chemistry.


[ Back to top ]
Examples -- Predator-Swarm Dynamics
The Predator-Preys Dynamics (PS) describes how a single predator interacts with a swarm of preys in a heterogeneous-agent system. We use the model introduced by Y. Chen and T. Kolokolnikov in their 2013 paper, "a minimal model of predator-swarm interaction". We consider two different kinds of Predator-Swarm dynamics, Predator-Preys Dynamics of first order system (PS1), and Predator-Preys Dynamics of second order system (PS2).
Results from learning PS1.

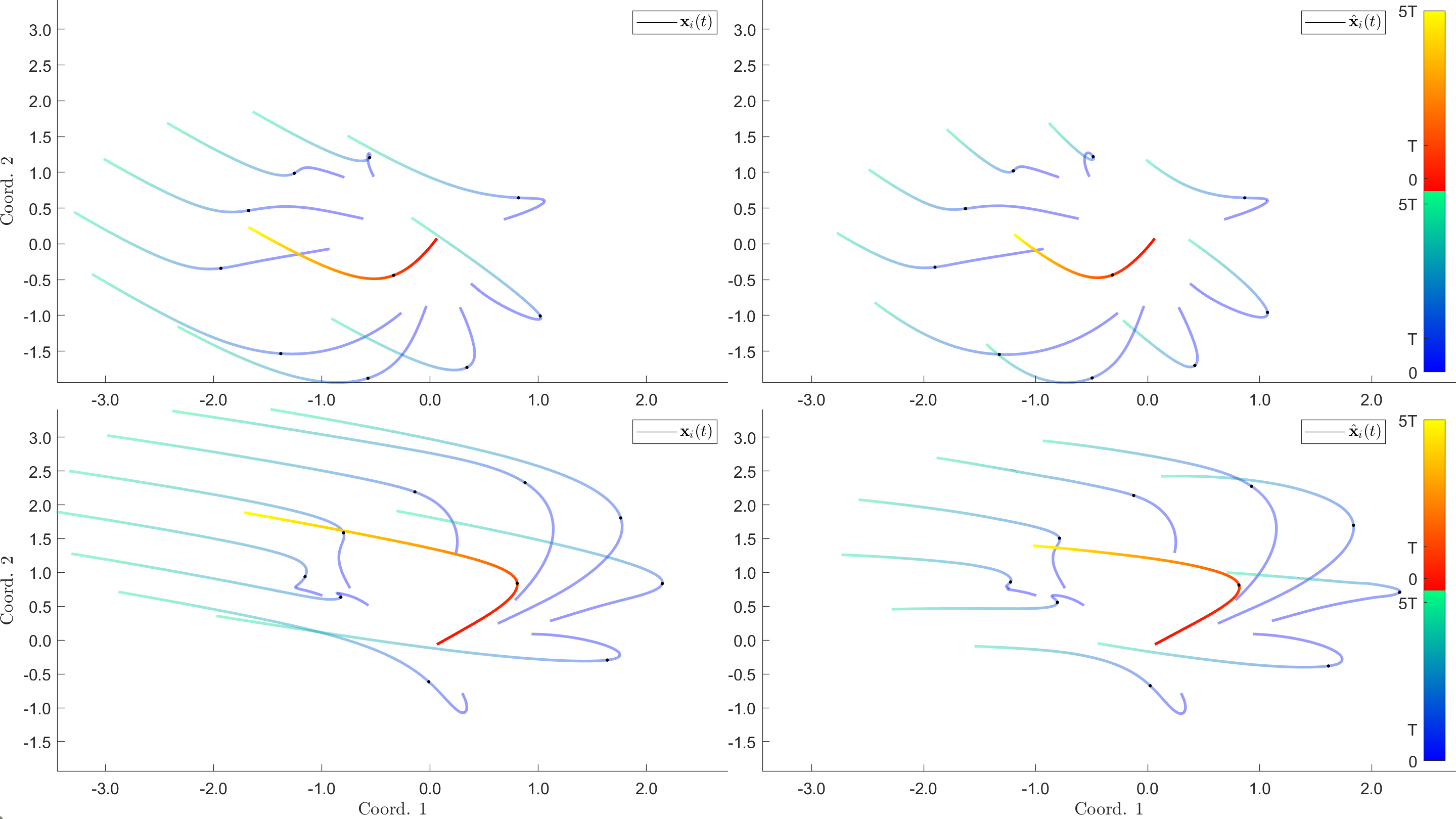
Results from learning PS2.


[ Back to top ]
Examples -- Phototaxis Dynamics
The Phototaxis Dynamics (PT) models how phototatic bacteria moves toward or away from stimulus of light. We use the model introduced by S. Ha and D. Levy in their 2009 paper, "particle, kinetic and fluid models for phototaxis".



[ Back to top ]
Examples -- Cucker-Smale Dynamics
The Cucker-Smale Dynamics (CS) models how flocking is formed. F. Cucker and S. Smale in their 2007 papers, "on the mathematics of emergence" and "emergent behavior in flocks", introduced such elegant and simple alignment model to describe the flocking formation.
Results from learning CS.


[ Back to top ]
Examples -- Self-Propelling Particle Dynamics
The Self-Propelling Particle Dynamics covers a wide range of collective dynamics, which models particle dynamics where an individual particle can provide self-accelerating and self-decelearting force as well as collective interaction with other particles. We consider here two kinds of self-propelling particle dynamics: one is the fish milling model in 2D, the other one is the fish milling model in 3D within a fluid envrionment.
Fish milling model in 2D (FM2D) describes how these self-propelling particles form milling pattern in 2-dimensional space. We use the 2006 paper by M. R. D'Orsogna, Y. L. Chuang, A. L. Bertozzi, and L. S. Chayes, "self-propelled particles with soft-core interactions: patterns, stability, and collapse", and a follow-up paper in 2018, by Y. L. Chuang, M. R. D'Orsogna, D. Marthaler, A. L. Bertozzi, and L. S. Chayes, "state transitions and the continuum limit for a 2D interacting, self-propelling particle system".
Fish milling model in 3D (FM3D) within a fluid envrionment describes how self-propelling swimmers display corresponding emergent behavior (flocking or milling) in a fluid medium. We use the paper by Y. L. Chuang, T. Chou, M. R. D'Orsogna, "swarming in viscous fluids: three-dimensional patterns in swimmer- and force-induced flows", in 2016.
Results from learning FM2D.


[ Back to top ]
Examples -- Synchronized Oscillators Dynamics
The Synchronized Oscillators Dynamics models how a system of agents swarm and have their internal states locked in synchronization. We use the model proposed by K. P. O'Keeffe, H. Hong, and S. H. Strogatz, in their 2017 paper, "oscillators that sync and swarm". It is a combination of swarming in space and synchronization of phases or other internal states. For other purely synchronization models, please see S. H. Strogatz's review paper, "from Kuramoto to Crawford: exploring the onset of synchronization in populations of coupled oscillators", in 2000.
Results from learning SOD.

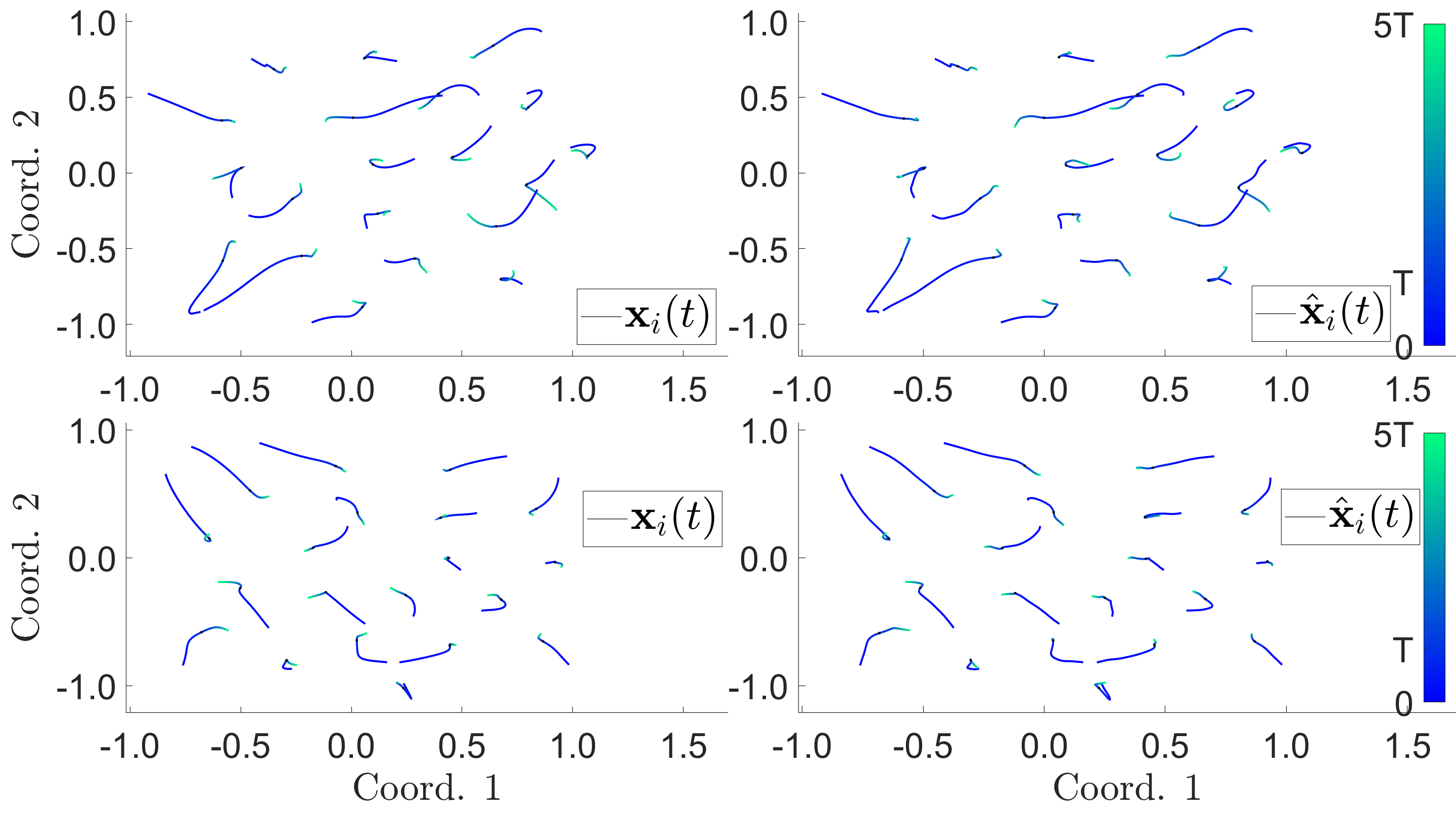
[ Back to top ]
Examples -- Simulated Gravitational Dynamics in the Solar System
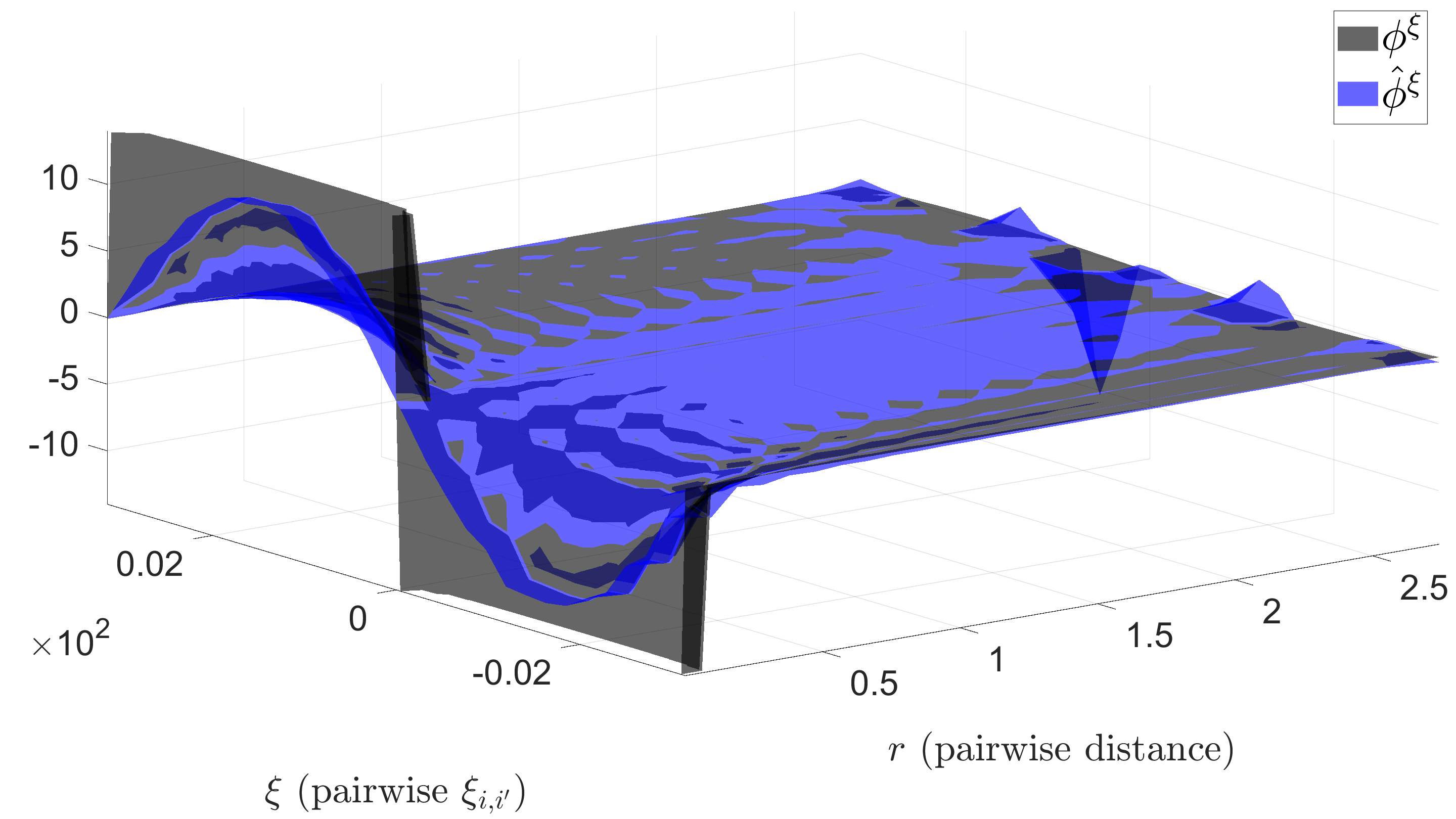
The planetary movement of astronomical objects in our Solar system can be considered as a collective dynamics with a simplified Newton's gravitational law (see [3] for details). We consdier here the inner Solar system with 5 astronomical objects (AOs): Sun, Mercury, Venus, Earth and Mars. And we study the learnability of such interacting system without knowing that the planetary orbits are elliptical or the form of the gravitatoinal force having the famous ''1/r^2'' form. We learn the interaction laws as type-dependent functions in a non-parametric fashion all together (a total of N^2 of them).
Results from learning GSS.


We discovered from our learned interaction kernels that, these estimated interactions share a common kernel. We use a de-couping procredue detailed in [3] to learn the masses of each Astronomical Object (AO), the shared kernele, which is the Newton's 1/r^2 form, and use it to clean up the estimated kernels.
Results from de-coupling the estimated interaction kernels.



[ Back to top ]
Examples -- Flocking with External Potential
The Viscek model and Cucker-Smale model provide a basic idea how alignment in the velocity space produces flocking. However these models might have the birds colliding into each other. The two Cucker-Dong models use energy-based repulsion to prevent the birds from colliding into each other. Using the idea that combining alignment-based forces with energy-based forces, the paper, Flocking hydrodynamics with external potentials (link here), by R. Shu and E. Tadmor, discusses flocking with a presence of external energy potential. It also extends the restriction on the alignment-based interaction to discuss condition on flocking.
Results from learning FwEP.



[ Back to top ]
Examples -- Anticipation Dynamics
The paper on flocking with external potential offered a starting point for dynamics to have both energy-based and alignment-based interactions together. However, the energy-based interaction from paper is only a positive constant, providing only attractive force, which is not decaying. In order to discuss a more complicated situation, and possibly including the Cucker-Smale model as a special case, the paper, anticipation breeds alignment (link here), by R. Shu and E. Tadmor, uses an anticipated Hamiltonian energy to derive a model with both energy-based and alignment-based interactions. And condition on flocking is also discussed.
Results from learning AD.



[ Back to top ]
Examples -- Celestial Dynamics in the Solar System from JPL Data
Understanding celestial mechanics (how stars move) has been an important and inspiring subject for research. We begin our research on celestial dynamics from the JPL development Ephemeris (accessible from NASA JPL's Horizons website). Results will be discussed when the paper is submitted.
[ Back to top ]
Examples -- Dynamics on non-Euclidean Manifold
Collective Dynamics constrained on a non-Euclidean manifold is an interesting subject, which has been gaining increasing amount of attention. It is a intruiging combination of differential geometry and dynamical systems. Our research investigates a couple first order dynamics (OD and LJ) evolving on several prototypical manifolds (S^2 and Hyperbolid Space). Results will be discussed when the paper is submitted.
[ Back to top ]
